Estimation Machinery
K5 Biases, Correspondences and Outliers
1 偏差
假设一个带有偏差的系统:
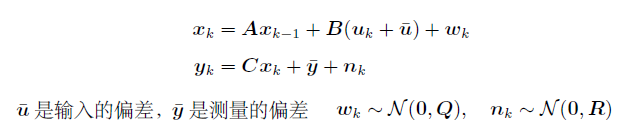

无偏:多次取样后,the mean of the estimator will converge to the true value that we want to estimate.
一致:多次取样后,估计协方差收敛于样本的(真)协方差
这个系统的无偏性和一致性不再存在:
假定k=0时无偏一致,可得k=1时是有偏不一致的:

需要修正卡尔曼滤波器,得到无偏一致的估计:
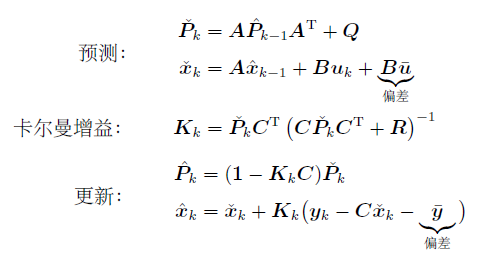
结论:
修正的过程中,我们需要知道偏差的精确值。但是,这多数情况下不可能,所以要对两种偏差进行估计。
输入偏差
假定测量偏差为0,只考虑输入偏差。
增广(augmented)状态x的形式:
即 将输入偏差 $\overline u$ 也作为需要估计的状态 和原来的 $x$ 组合成新的增广状态。
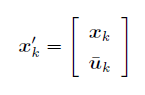
运动模型:

观测模型::
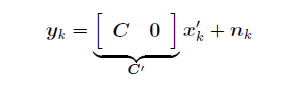
这里可以继续讨论存在唯一解的条件(参照唯一解),即观察能观性矩阵。
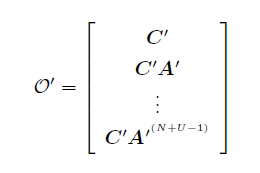
测量偏差
增广(augmented)状态: 将测量偏差 $\overline y$也加入到 $x$中
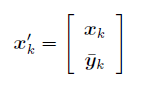
运动模型:
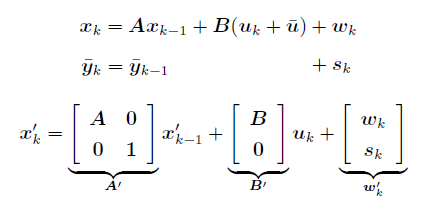
观测模型:
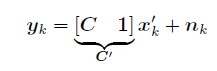
SLAM:同时定位与地图建立。“定位”对应车的状态,“地图”对应路标点的位置。
例:不能观的系统:观察能观性矩阵发现不满秩,零空间是线性生成空间($O’v=0$的解不唯一)

意味着当我们同时移动推车和路标(向左或向右移动)时,测量不会发⽣改变。
- Batch:左侧的矩阵不能求逆。但是我们知道,对于每⼀个线性方程组Ax = b,要么没有解,要么有唯⼀解,要么有无穷多组解。在这种情况下,我们的线性方程组是有无穷多组解而不是唯⼀解的。
- KF:我们需要对状态有⼀个初始的估计。我们最终得到的解依赖于初始条件的选取。换句话说,在初始时刻引入的偏置,将⼀直存在于系统中。
2 匹配
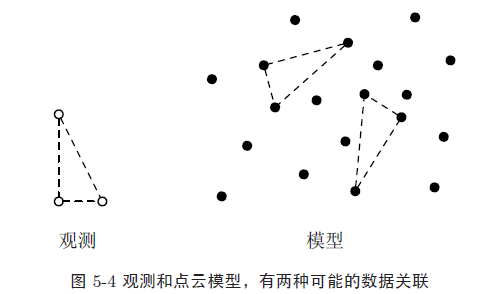
数据关联问题就是找出每⼀个测量信息对应于模型中的哪⼀部分。如果匹配不正确,可能会导致结果不收敛。
外部数据关联
例如,⼀些观测物体被涂上了不同的颜色,而通过立体相机观测到的这些物体,可以利用颜色信息来进行数据关联。颜色信息在估计问题中也就不会再用到。诸如视觉条形码,特定频率的信号或者编码信息(如GPS 卫星)也是外部数据关联。
内部数据关联
比如谷歌最近有的 扫地标判断位置 。
3 外点
⼀种常见的⽅法(在⼀维度数据中)是将超出平均值三个标准差的测量值作为外点。
处理外点的两种最常用方案:RANSAC, M-估计。两种方案可以单独使⽤或串联使用。
RANSAC

注意是计算内点的残差和。
除了简单的找2D直线,也可以运用在3D直线中:Fundamental Matrix
Iterations
设每个点是内点的概率为 w = 内点数量/总数量,拟合模型需要n个点 (直线需要两个点 n=2),需要拟合k次。
那么:
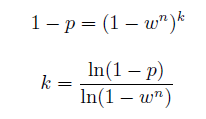
p(k次都不成功) = 1-p(k次中有一次成功) = (p(这次不成功))^k = (1-p(这次成功))^k
p(这次成功) = p(选的n个点都是内点) = w^n
M-Estimation / Robust Estimation
在NLNG-MAP中的关于e的二次型 non-robust的原始目标函数
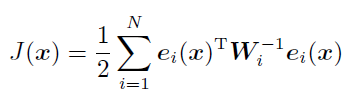
现在令:

得到新目标函数
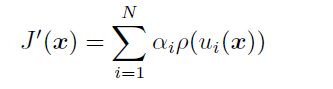
满足条件的p(u)有很多,如:
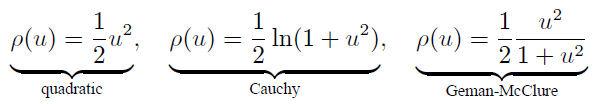
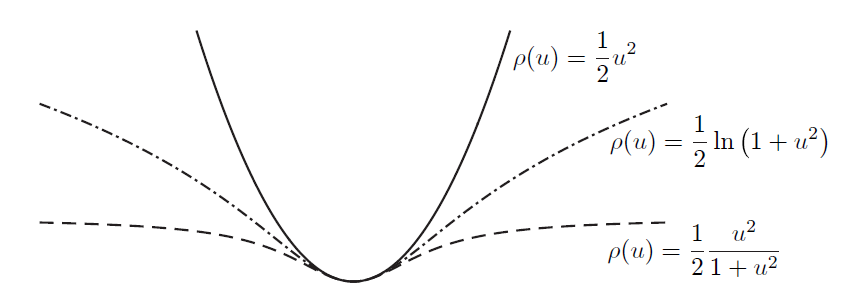
其中比二次函数增长慢的成为鲁棒代价函数。
因为增长较慢,当e很大(外点)时,权重不会很大,影响力减弱。
梯度:
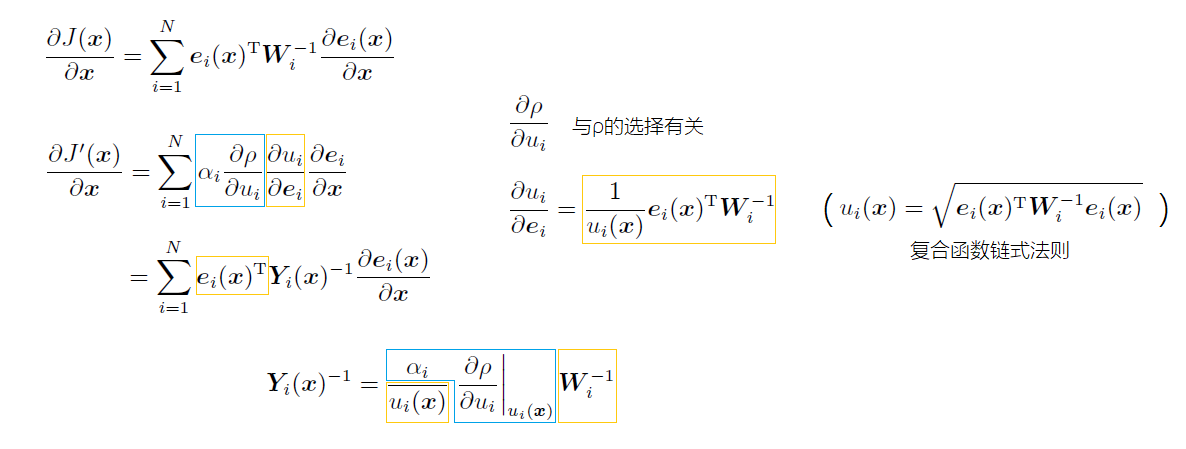
其中 $W_i$是constant的,但 $Y_i$取决于 $u_i$所以不是constant了。这导致每次协方差矩阵都会变化。
可以用迭代的方法:用上一个 $x_k/x_{op}$计算 $Y$。
即迭代重加权最小二乘法 IRLS
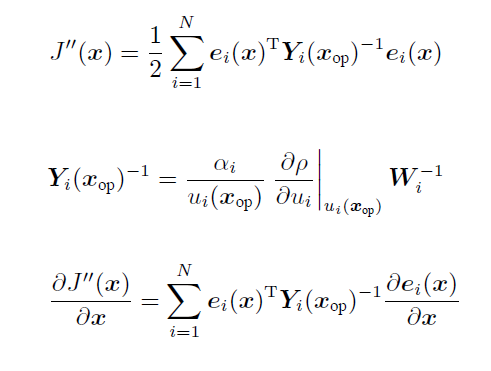
总结
- 总是有非理想的因素(例如偏差和外点),使得实际的估计问题与本书中纯数学的推导不同。这些非理想因素是实际应用中误差的主要来源。
- 在某些情况下,我们可以将估计的偏差叠加到估计框架中,而在有些情况不能这么做。这是由问题的能观性来决定的。
- 在大多数实际的估计问题中,外点是真实存在的,因此有必要使⽤某种形式的预处理(如RANSAC)以及鲁棒代价函数。
16.01.2021 完结
SER目录
| SER目录 | ||
|---|---|---|
| SER-1 | K2 - 基础概率论 | |
| SER-2 | K3 - LG系统下Batch/Smoother | |
| SER-3 | K3 - LG系统下Recursive Filter | |
| SER-4 | K4 - NLNG系统下Recursive Filter | |
| SER-5 | K4 - NLNG系统下Batch | |
| SER-6 | K5 - 偏差,匹配和外点 |