Estimation Machinery
K4 Nonlinear Non-Gaussian Estimation-1
上回总结
定义问题 LG系统下
批量方法Smoother
-> 批量处理方法的 MAP & 贝叶斯 得到同一个方程 (MAP是模,贝叶斯是均值)
-> Cholesky分解解方程HWH=LL 前向后向 得到一些关于L的迭代方程组
-> 可以继续变形 消去L 变成RTS Smoother(4+1信息形式/5+1经典形式)
递归方法Filter
-> 递归的 MAP & 贝叶斯
-> 得到4/5个方程 叫做 卡尔曼滤波器(和RTS中前向部分的一样)
这回内容
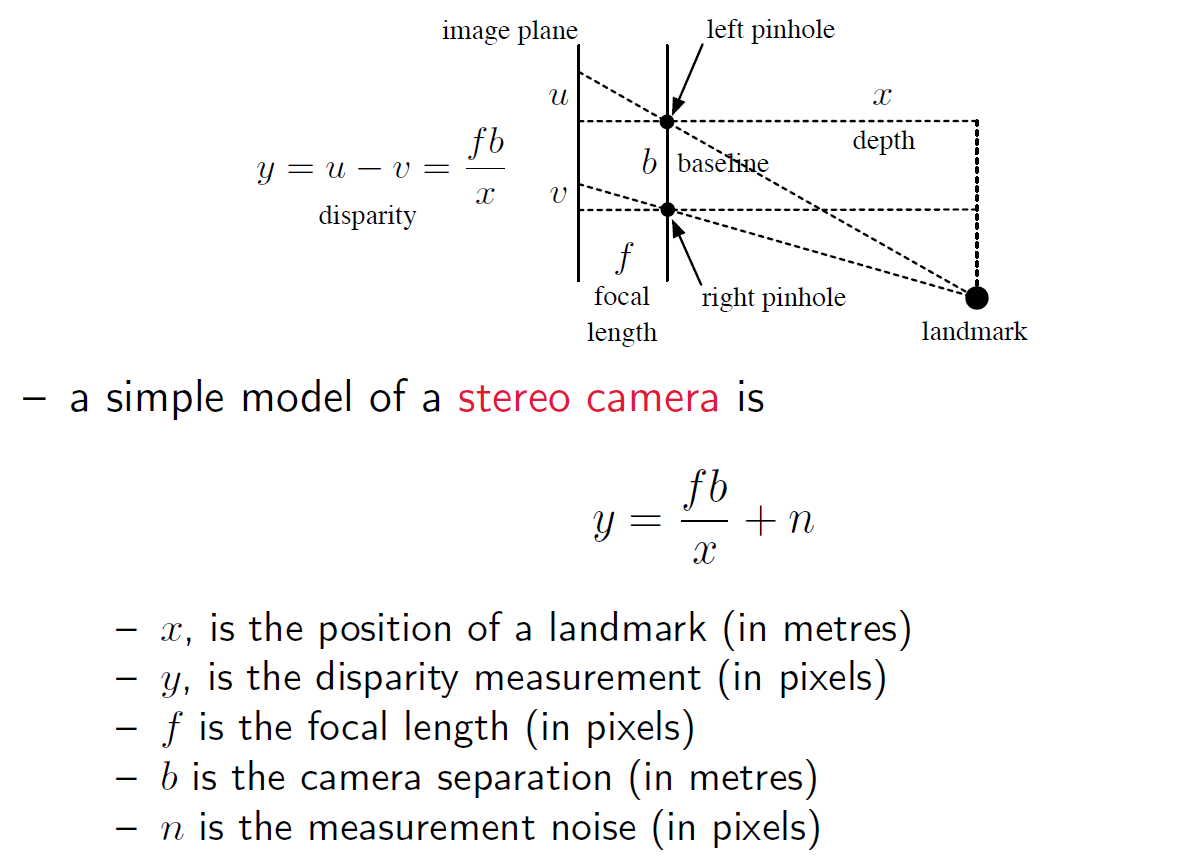
NLNG系统下,问题setup:【1】中介绍了双目相机用到了非线性模型,【2】是运动和观测方程。
- 贝叶斯滤波器:基于贝叶斯公式,只是理想的抽象数学模型。
- 扩展卡尔曼:线性化以后代入贝叶斯滤波器,效果不一定好,不一定收敛。
- 广义高斯滤波器:抽象模型,扩展卡尔曼是线性化的结果,还可用其他方式做非线性处理。
- 迭代扩展卡尔曼:仍然考虑线性化,但反复迭代EKF的线性化操作点,使结果收敛。
- 粒子滤波:考虑蒙特卡洛
- SP卡尔曼:考虑SP变换
总结:比较各种滤波器
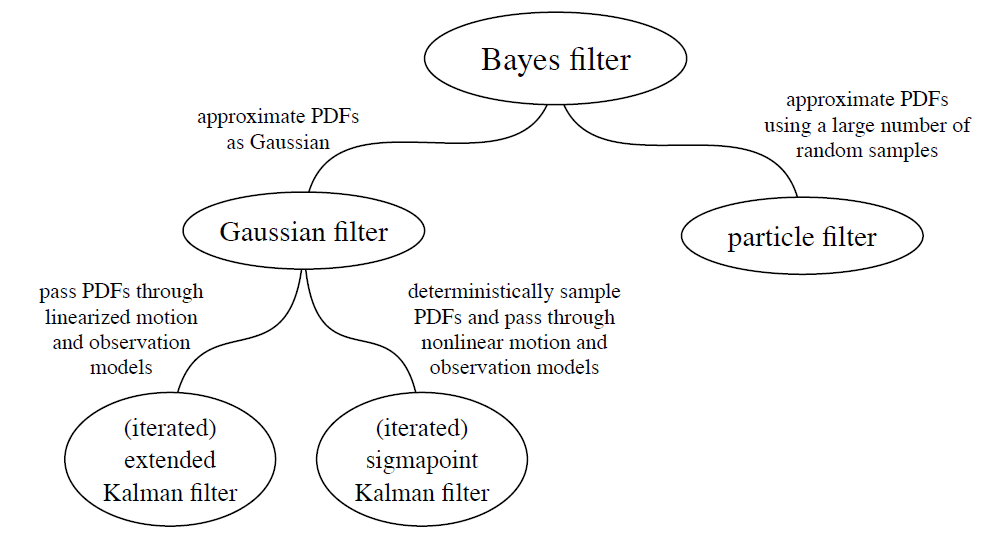
注:prior/posterior
上一时刻 这一时刻运动估计 这一时刻观测修正 用法1 k-1 posterior prior posterior 用法2 prior belief/estimation predicted belief posterior belief
Setup 1
$\frac{b}{x} = \frac{b-v+u}{f+x}$
Bayesian
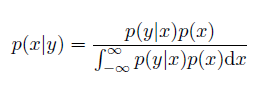
Bayesian Framework
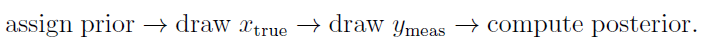
We start with a prior. The ‘true’ state is then drawn from the prior, and the measurement is generated by observing the true state through the camera model and adding noise. The estimator then reconstructs the posterior from the measurement and prior, without knowing x_true.
MAP
以前已经说明过:
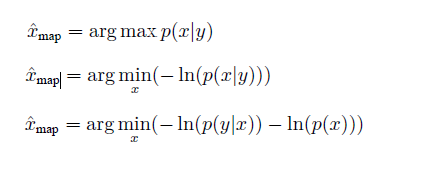
for the example of stereo camera:
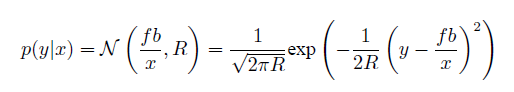
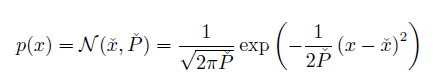
so:
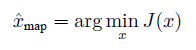
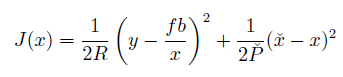
Setup 2
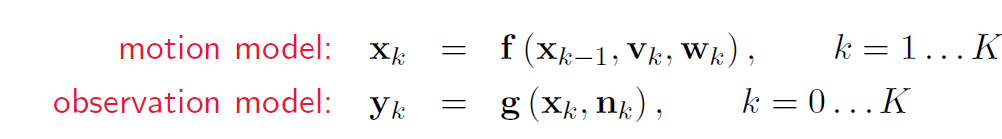

Markov Property
the conditional PDF of future states of the process, given the present state, depend only upon the present state, but not on any other past states, i.e., they are conditionally independent of these older states. Such a process is called Markovian or a Markov process. 在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的。
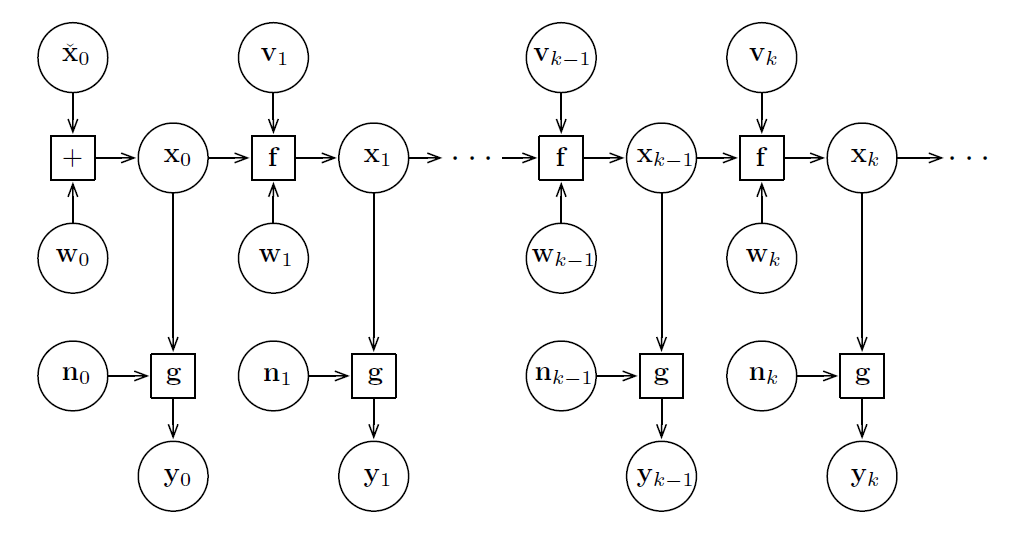
1 Bayes Filter
目的:计算 belief function
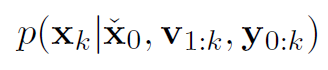
第(1)步:用贝叶斯公式展开
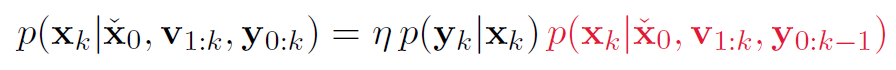
第一步原理:贝叶斯公式:
here, $x = x_k \qquad \qquad y = y_k \qquad \qquad z = x_0, v_1:v_k,y_0:y_{k-1}$
其中p(y|z)是常数,因为当前的测量只和当前状态有关,和{输入,之前的测量,之前的状态}无关。
第(2)步:计算p(x|z)
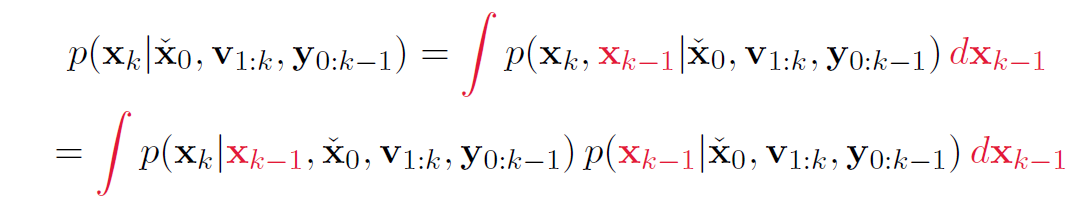
第二布原理:全概率公式 + 条件概率公式

第(3)步:简化积分中的两项:hidden state / inverse of marginalization

第三步原理:马尔可夫性质
当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态。
第(4)步:联立

结论:
$x$实现递归推导。
这个状态 = 用g测量得矫正 用运动模式f的预测 上一个状态
是一个predictor-corrector的形式,和卡尔曼滤波器一样。矫正和预测只和当前和上一个状态有关。
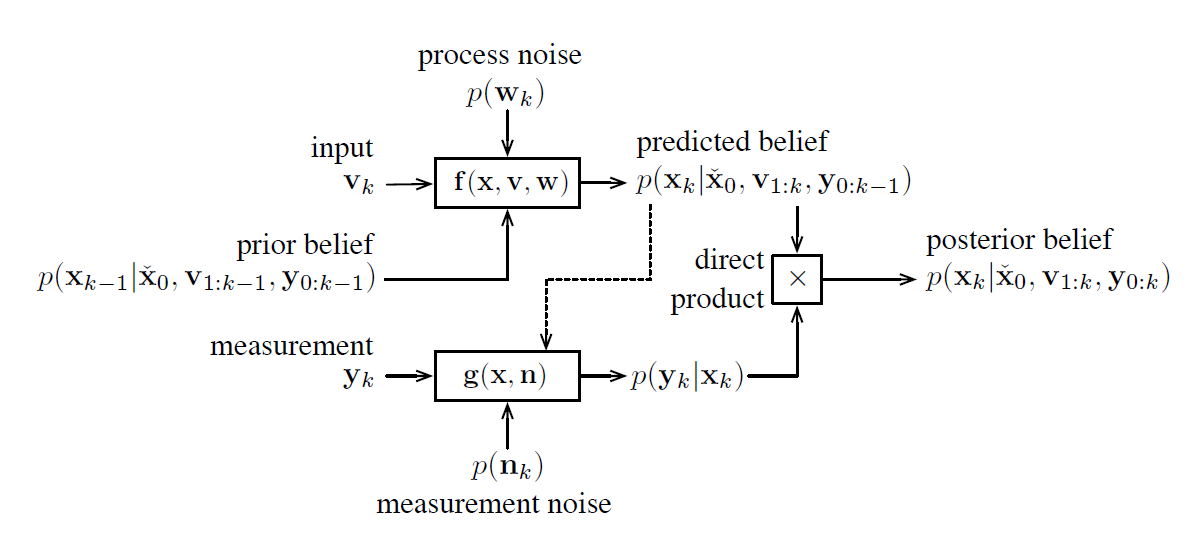
但只是一个数学模型,除线性高斯系统中,不可能实践。
- infinite amount of memory: 需要用于储存v1-vk, y0-yk的无限储存空间。
- infinite computing resources: 计算积分的代价很大。
2 Extended Kalman Filter
先上结论以及与LG系统下的KF的比较:

EKF是BF的特殊情况(前提/假设):
-
prior是高斯分布。
-
两个噪音w,n是零均值高斯分布,且无关。
-
运动和观测方程f,g被线性化。(线性化方法在SER-1-2.2.8中提到)
-
运动和观测方程的线性化操作取在如下两个点上:
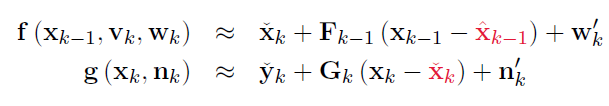
(1) 线性化f,g
从 setup 2 的运动观测方程开始。
线性化的操作点见上方4

(2) 运动和观测 $p(x_k | x_{k-1},v_k), p(y_k | x_k)$
求p就是计算 x_k,y_k 的均值和协方差
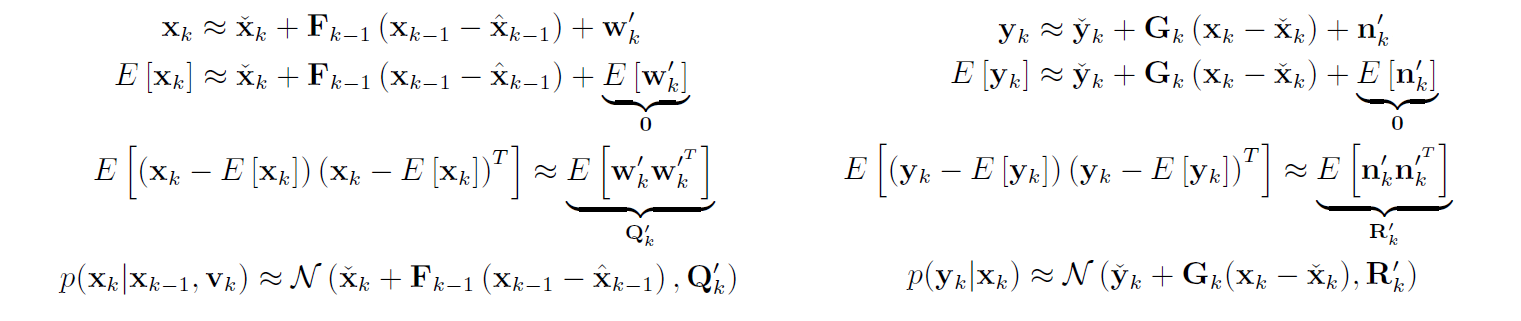
协方差部分根据定义 w’ = 雅可比矩阵 × w, 即 E[w’w’^T] = J·E[ww^T]·J^T = J·Q·J^T = Q’。同样得到n。
(3) 代入BF
上一节推导的BF:

代入后得到:
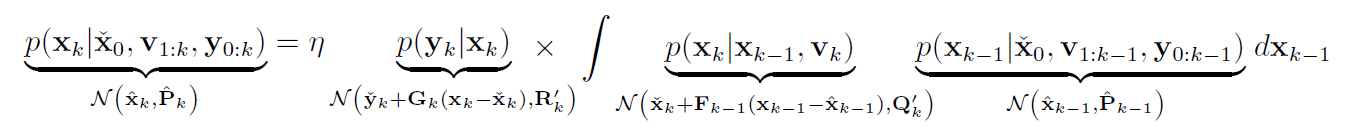
(4) 计算BF积分部分
积分部分使用 SER-1-2.2.8 中的结论: $y \sim \mathcal{N}(\mu_y, \Sigma_{yy}) = \mathcal{N}(g(\mu_x), R+G\Sigma_{xx}G^T)$
将服从⾼斯分布的变量传⼊⾮线性函数中,可以看到积分仍然是⾼斯的。
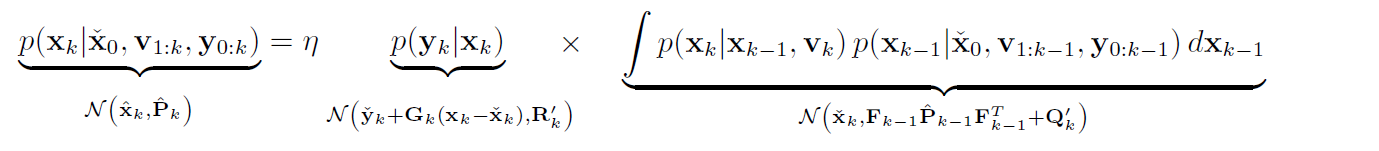
(5) 计算整个BF
需要用到 SER-1-2.2.6 归一化积的结论:
即K 个⾼斯概率密度函数的归⼀化积,仍然是⾼斯概率密度函数。
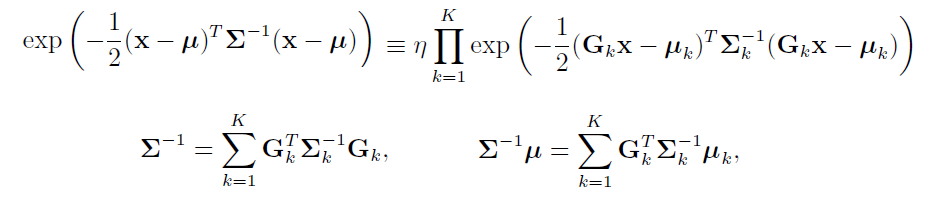
在(iv)中两个乘积仍然是高斯的。这一步就变成了求G1,G2,μ1,μ2,Σ1,Σ2。(为了防止字母混淆,这边用加粗表示)
A) (iv)中第二项(积分部分)已经直接说明了$\mathbf{μ}_2=\check{x_k}$ , $\mathbf{Σ}_2 = Q’+FPF = \check{P}_k$ 和 $\mathbf{G}_2 = \mathbf{I}_d$
B) (iv)中第一项展开它的指数部分 得到 $exp(-\frac{1}{2}(y_k-\check{y_k}-G_k(x_k-\check{x_k}))^T(R’_k)^{-1}(…))) $
化到 (Gx-μ)Σ$^{-1}$(Gx-μ)形式。得到$(\mathbf{G}x-\mathbf{μ}) = G_kx_k-(y_k-\check{y_k}+G_k\check{x_k})$ 。即 $\mathbf{μ}_1=y_k-\check{y_k}+G_k\check{x_k}$, $\mathbf{Σ}_1 = R’_k$ 和 $\mathbf{G}_1 = G_k$
代入归一化积结论中。
(6) 使用SMW
(7) 定义卡尔曼增益
解出归一化积中的μ,Σ。
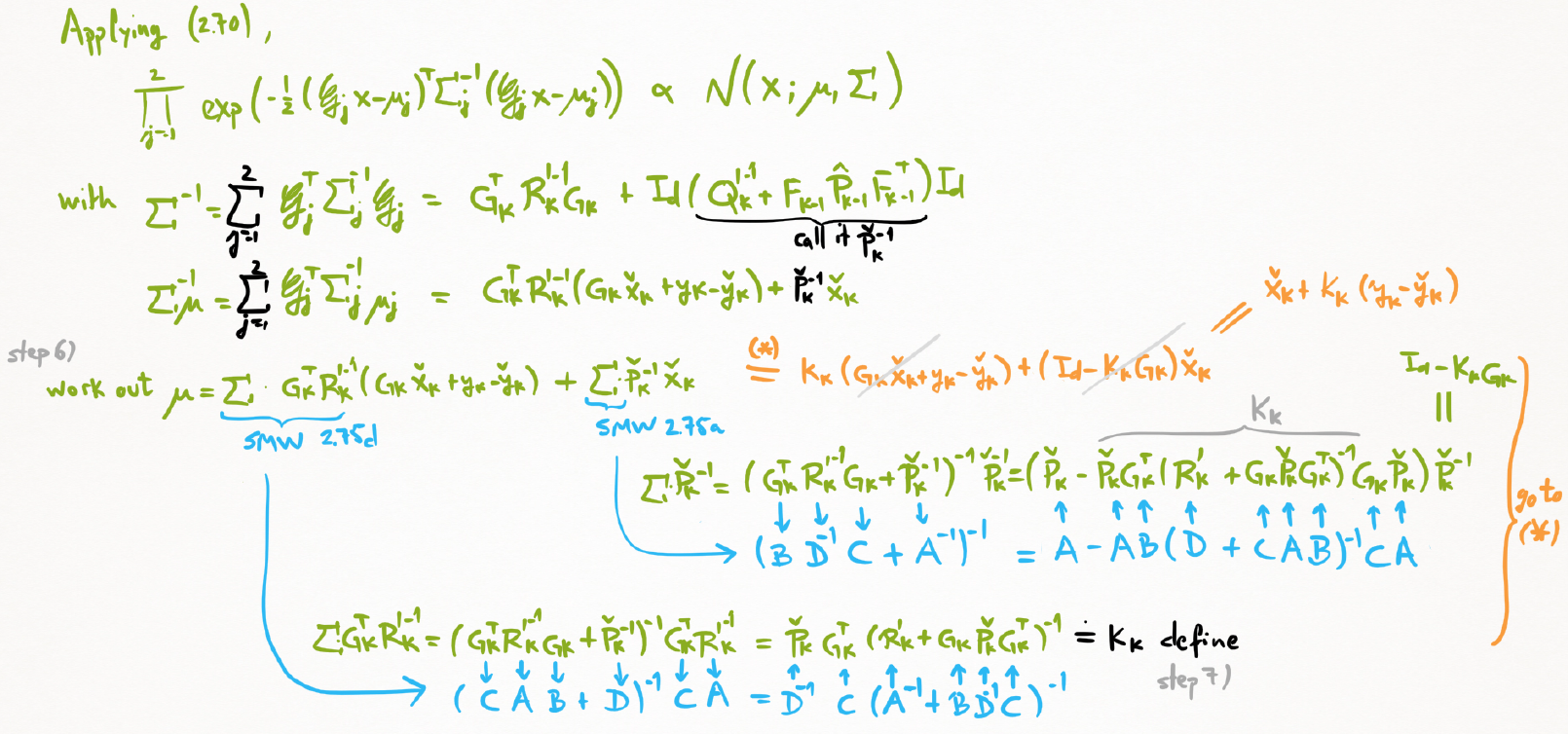
(8) 代入整理,得到均值和协方差
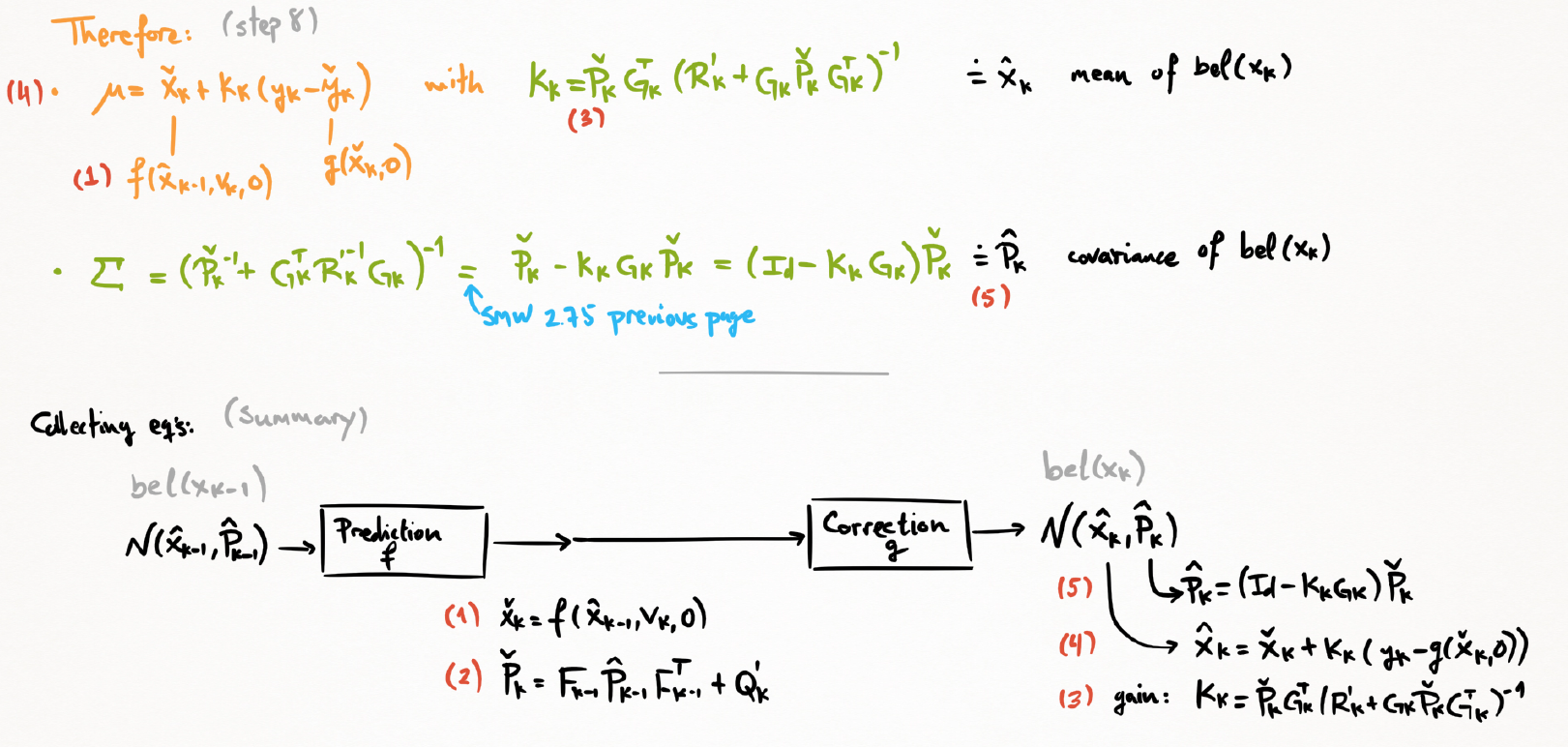
结论

-
有着和KF相似的结构,两点不同
- 通过非线性运动模型得到先验均值
- 更新过程使用先验均值和非线性观测模型得到观测的预测值
- 协方差矩阵 Q’ ,R’ 中蕴含了雅可比矩阵 J (Q’=JQJ$^T$)
-
不能证明对于非线性系统一定适用(收敛)
因为线性化的操作点是估计均值点,并非实际真值。会导致在一些情况中EKF偏离很大,变成有偏的, 不一致的。
3 Generalized Gaussian Filter
(1) 上一时刻的置信函数
(2) 通过非线性运动模型预测得到这一时刻的先验 (即加上这一时刻的输入 vk ,得到 xk)
(3) 运动和观测的联合分布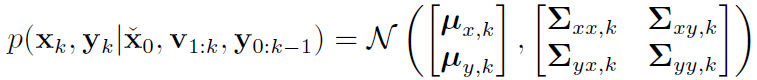
(4) 这一时刻的置信函数通过高斯推论得到
拆开联合分布 $p(x,y \mid z) = p(x \mid y,z) \cdot p(y \mid z) $得到$p(x \mid y,z)$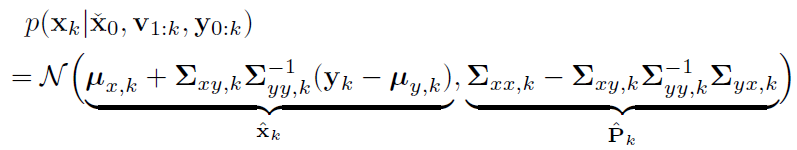
问题转换成:
求解需要的5个项 (μx_k, μy_k, Σx_k, Σy_k, Σxy_k)
(1) μx_k 和 Σx_k 通过运动模型进行预测,即为$\check{x_k},\check{P_k}$,就是上面的(2)
(2) 定义卡尔曼增益
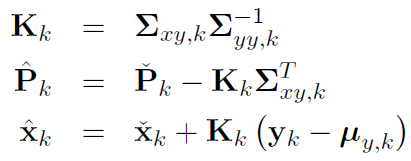
(3) μy_k, Σy_k 和 Σxy_k 可通过多种近似方式得到。(在EKF中就使用了线性化的方式)
看着整个过程和LG系统中批量处理时的贝叶斯推断很像,先找到先验均值协方差,再找到观测均值协方差,再找到联合分布的协方差,就能通过高斯推断写出后验的均值协方差。
4 Iterated EKF
(1) 线性化观测方程 见 EKF(1)&(2)
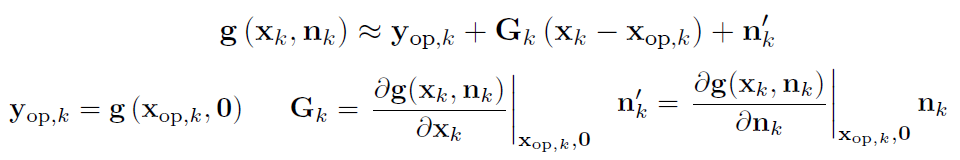
(2) 联合分布
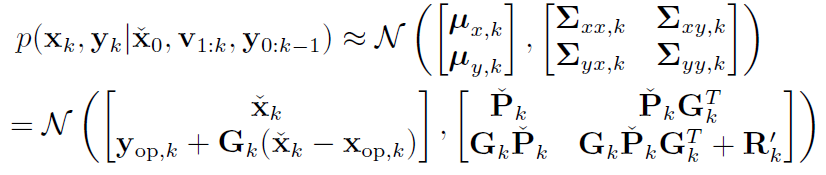
(3) 高斯推断 以及 定义卡尔曼增益
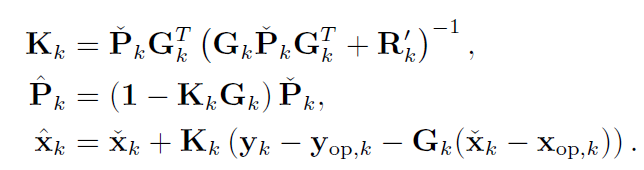
(4) 第一次迭代 = EKF: 令 $x_{op,k} = \check{x}_k$
(5) 第n次迭代: 令 $x_{op,k} = \hat{x}_k^{(n)}$
(6) 当收敛到足够小时停止迭代
结论
在单个时间步长的迭代下,IEKF对应全后验概率的极大值,是一个MAP估计,计算的是模,而不是均值。
x Transforming PDFs
对非线性函数处理的手段:
-
linearization: 见EKF/IEKF
以x的均值点作为操作点,进行线性化后得到y的分布。得到高斯分布。
但事实上x的均值点,不一定是y的均值点。而且x的均值点还是一个估计值,可能是错误的。
而且高斯分布非线性变换后本身不再是高斯分布。另外线性化本身存在误差(局部范围近似)。
-
Monte Carlo sampling
大量采样,大数定律,依概率收敛。
计算量随纬度指数增长。采样量越大越准确。可以得到任何分布。
-
sigmapoint transformation(SP变换/无迹变换)
线性化和蒙特卡洛的折中。
选定输入分布的几个点(Sigma Point),计算这几个点的非线性变换,构建输出分布。得到高斯分布。
(1) 对于L维高斯分布选取 2L+1 个点
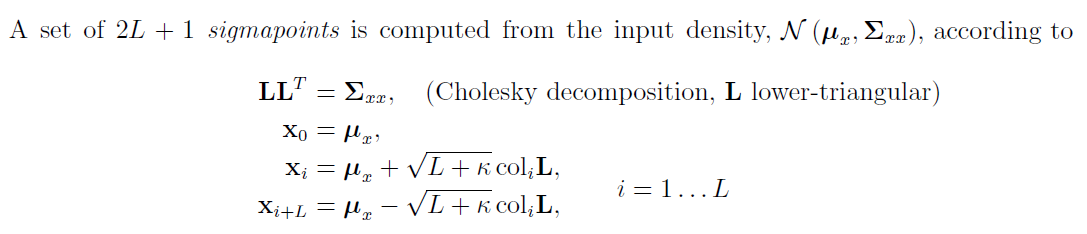
选取的这些点能通过以下方法还原到矩(均值和方差):
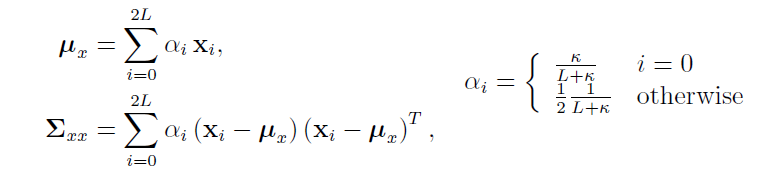
(2) 将每个点代入 y = g(x) 得到非线性变换
(3) y的均值和方差用类似的方法得到,并得到y的高斯分布:
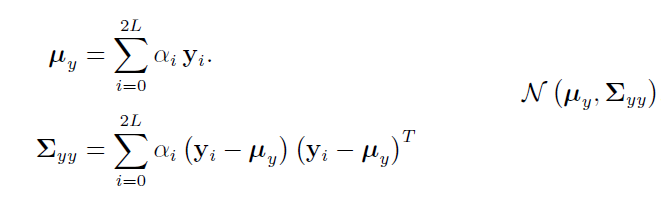
5 Particle Filter
唯一一种可以处理NLNG系统的实用技术。也称为 自举算法 bootstrap algorithm, 凝聚算法 condensation algorithm 等等。
(1) 从先验和运动噪声的联合分布中抽取M个样本
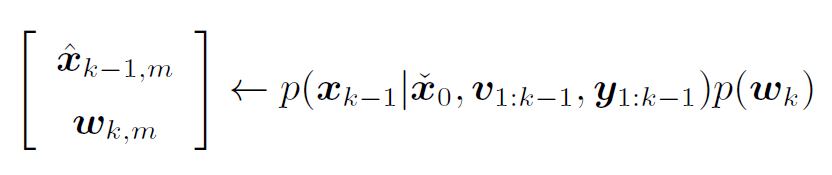
(2) 使用v_k得到后验PDF (可以理解为将每个 $\mathbf{\hat{x}}_{k-1,m}$ 代入运动方程 f() 得到 $\mathbf{\check{x}}_{k,m}$)
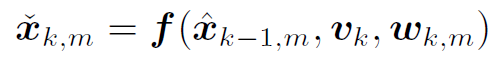
他们刻画了概率密度:
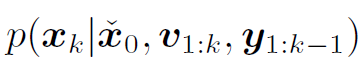
(3) 结合观测 y_k 对其进行矫正:
根据每个粒子的期望后验和预测后燕的收敛程度赋予权重:
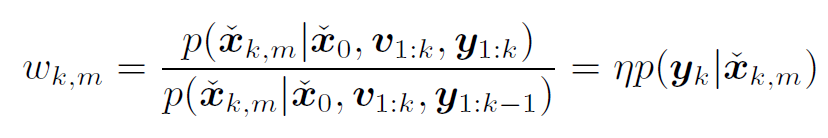
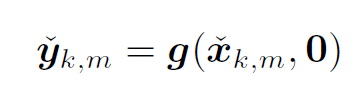
假设:
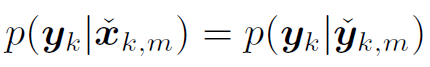
这个权重其实是这样算的:
1 根据运动方程我们得到了一堆 prediction $\mathbf{\check{x}}_{k,m}$, 根据这些代入观测方程能得到一堆 $\mathbf{\check{y}}_{k,m}$, 通过这些可以知道一个预测分布 $g(·)$ 。这个过程不需要知道 k 时刻的观测结果,完全是预测出来的。
2 另一方面,根据实际的 k 时刻的观测, $\mathbf{y}_{k}$是测量出来的,满足一个目标分布 $f(·)$。
也就是说预测分布中是没有 $\mathbf{y}_{k}$ 的,而目标分布中是带 $\mathbf{y}_{k}$ 的。也就是上方的 $\mathbf{w}_{k}$ 式子中分母分子的部分。
为了让预测分布贴合目标分布:$ f = \frac{f}{g} g$ , 其中 $ \frac{f}{g} = w$。
(4) 根据权重重采样:比如Madow Resampling
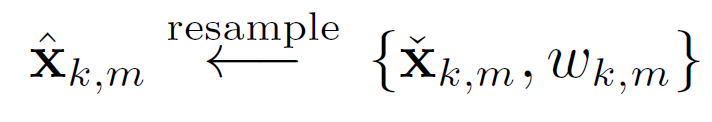
整个过程:
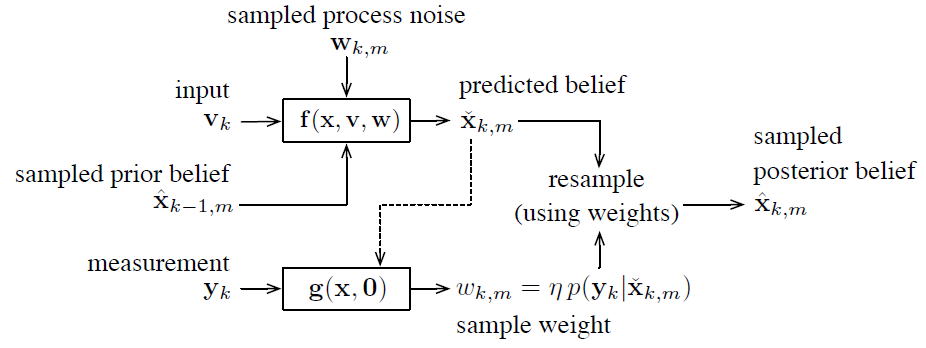
6 SP卡尔曼
预测步骤: 将先验置信度转换为预测置信度:
(1) 联合先验置信度(k-1时刻)和运动噪声(k时刻)
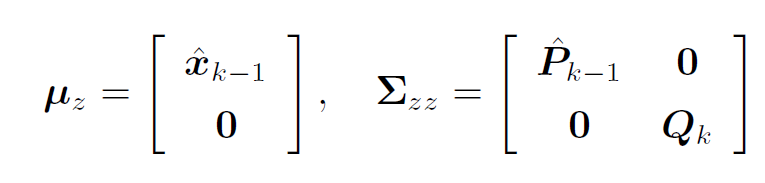
(2) 取Sigma Point
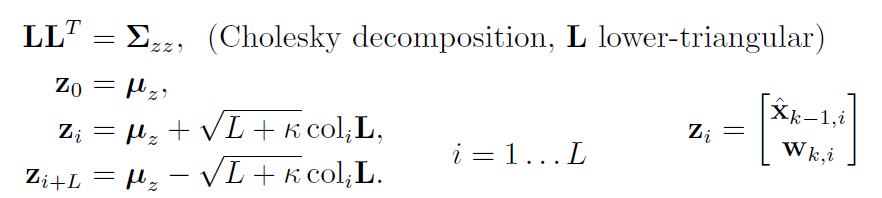
(3) 代入运动模型 得到每个变化后的Sigma Point:
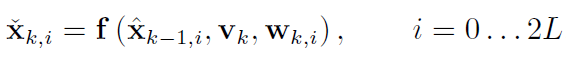
(4) 得到预测置信度:
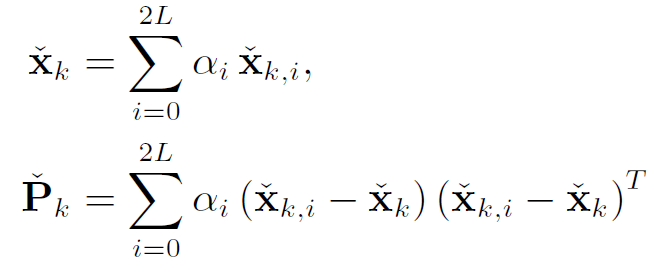
校正(观测)步骤:
(1) 联合预测置信度(k时刻)和观测噪声(k时刻)
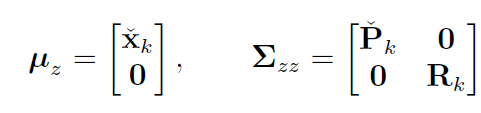
(2) 变换Sigma Point
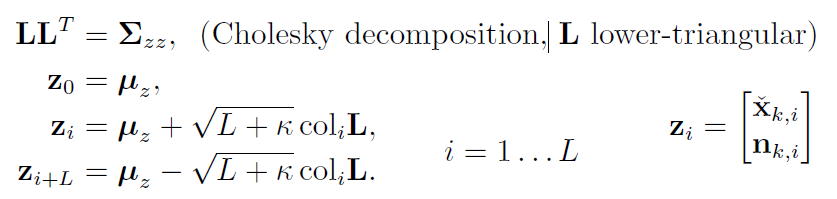
(3) 代入观测模型:
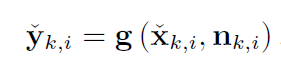
(4) 得到后验置信度:
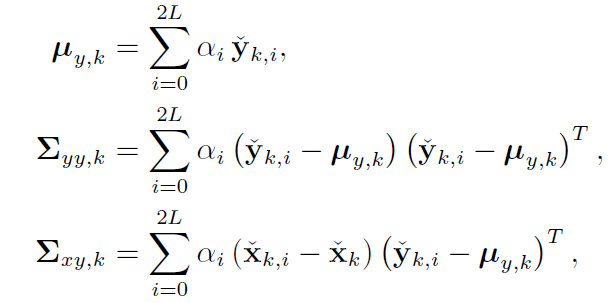
整理:
使用高斯滤波器的结论,代入
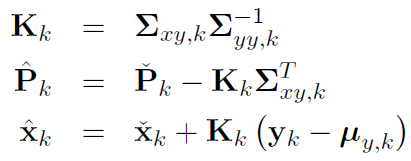
并且SPKF也可以迭代。
总结
| Filter | 分布 | 系统 | 效率 | 注 |
|---|---|---|---|---|
| KF | 高斯 | 线性 | 高 | 要求严苛 |
| EKF | 单峰,用高斯拟合 | 可导 (雅可比) |
高 | |
| IEKF | ’’ | ’’ | 迭代,略低于EKF | 收敛于模, 算力换准确度 |
| SPKF | 单峰,采样SP点,求矩, 用高斯拟合 |
不要求可导 | 略低于EKF, 但全是线代操作 |
|
| ISPKF | ’’ | ’’ | 迭代,低于SPKF | 收敛于均值, 算力换准确度 |
| PF | 任何分布 | ’’ | 低,暴力,随维度指数增长 |
完结撒花 30.12.2020
SER目录
| SER目录 | ||
|---|---|---|
| SER-1 | K2 - 基础概率论 | |
| SER-2 | K3 - LG系统下Batch/Smoother | |
| SER-3 | K3 - LG系统下Recursive Filter | |
| SER-4 | K4 - NLNG系统下Recursive Filter | |
| SER-5 | K4 - NLNG系统下Batch | |
| SER-6 | K5 - 偏差,匹配和外点 |