Estimation Machinery
K4 Nonlinear Non-Gaussian Estimation-2
上回总结
Recursive Discrete-Time Estimation
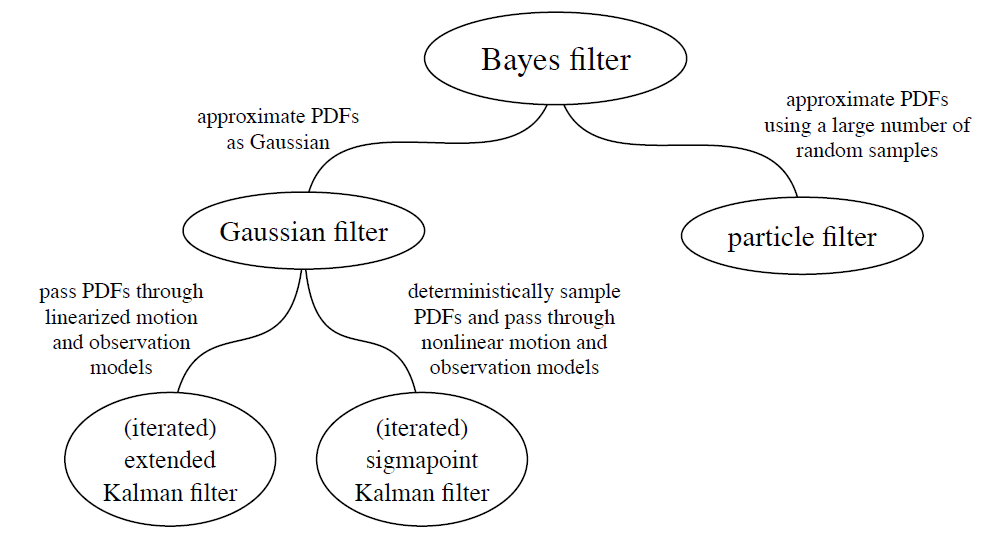
上回的滤波算法是由贝叶斯滤波推导而来,推导的过程中使⽤了马尔可夫假设来实现其递归形式。马尔可夫假设的问题在于,⼀旦估计器建⽴在该假设上,我们就⽆法摆脱它。这是⼀个不能克服的,根本性的制约因素。
这回内容
Batch Discrete-Time Estimation
-
MAP目标函数 J(x) = 1/2 u^2, 再通过下面的方法局部拟合,最后总结批量估计公式。
对于局部拟合给出三种方法:
-
Bayesian:和LG系统中基本相同,也和IEKF中基本相同(区别在于 在线和离线 / 递归和批处理)
MAP-Start
定义目标函数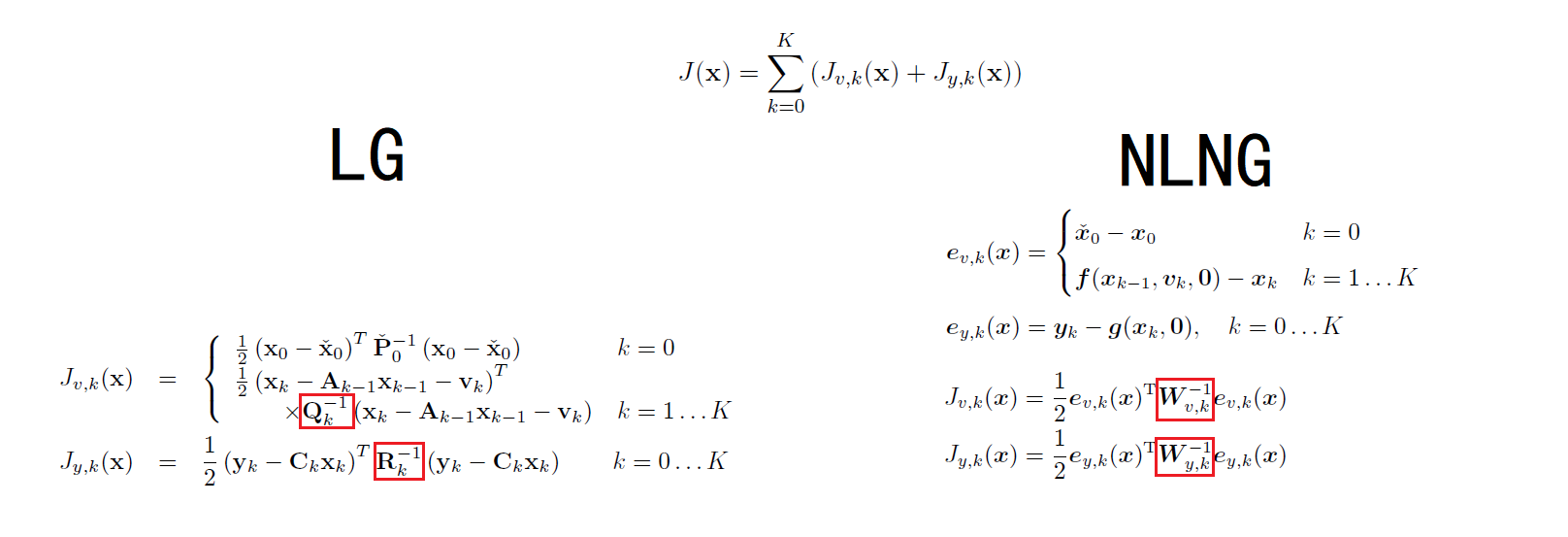
$W$ are the covariances of the measurement noises.
和LG的时候是相同的。
在NLNG中,这是关于$e(x)$的二次型,并非关于x的二次型。(因为 $e(x)=f(x_{k-1}) - x_k$ 并不一定是一次的, 即$f(x)$ 非线性。)
进一步可以把W通过Cholesky分解得到 $W=L^T L$, 令 $u(x)=Le(x)$ , 则 $J(x)=\frac{1}{2}u(x)^Tu(x)$。
非线性最小二乘问题 NLLS
- Newton’s Method
牛顿法的 J 不需要必须是最小二乘形式,任意的 J 都可以展开拟合。
选择操作点,在操作点用二次函数拟合(泰勒展开前三项, 注: 前两项是线性拟合),找到拟合的最小值处($x_{op} + \delta x^*$)为下一个操作点,重复直到操作点变化($\delta x^*$)足够小。
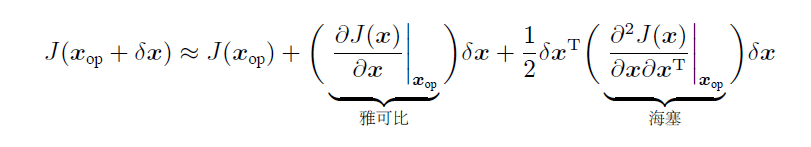
即 求$\delta x^*$的方程:(最小值即该点导数(梯度)为0,海塞矩阵正定。)
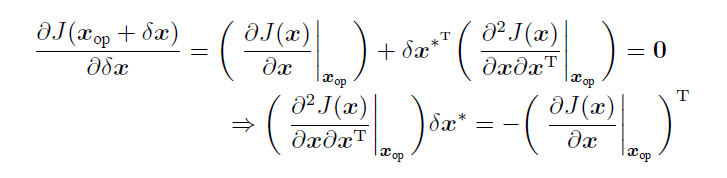
最后的形式为 $H \cdot s = -g$, 即 海塞矩阵H * 步长step = - 梯度g(雅可比)
特点:
- 局部收敛,局部最小值
- 收敛速度二次的(比梯度下降快)
- 海塞矩阵复杂,消耗算力,现实中应用困难
- Gauss-Newton Method
如果 J 是最小二乘形式的。
目的是简化二阶导的海塞矩阵
方法一:
假定操作点十分接近最小值点。
$J(x)=\frac{1}{2}u(x)^Tu(x)$
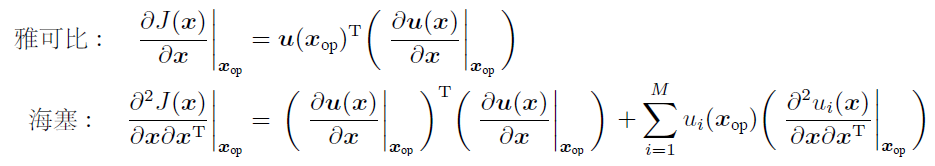
现在直接对 $J(x)$在操作点 $x_{op}$处求导。一阶导数(雅可比)即复合函数求导,链式法则。二阶导数(海塞)即对雅可比再次求导,乘法法则。
在极小值附近,$u(x)$很小,接近0。海塞中的第二项可忽略。代入$H \cdot s = -g$中得到:
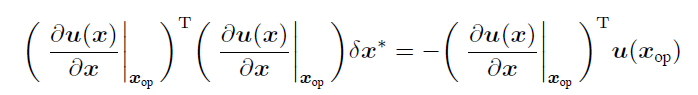
方法二:
对 $u(x)$进行泰勒展开(之前是对 $J(x)$),
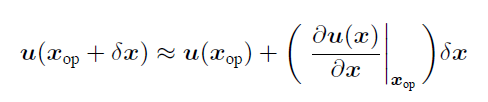
对展开的结果平方(代入 $J(x)$)。
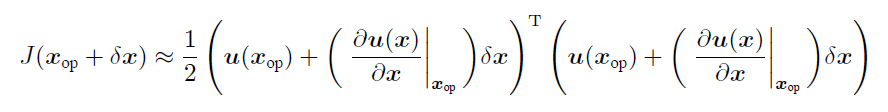
在对 $\delta x$求导,可看成复合函数链式法则/也可看成乘法法则。
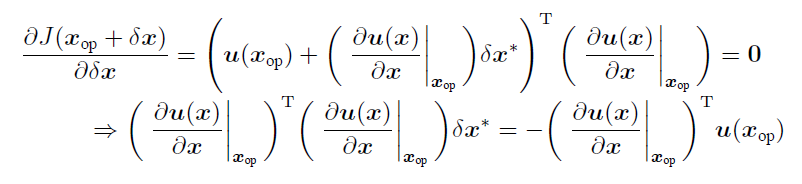
$H \cdot s = -g$
改进:
因为对海塞进行了近似,导致不一定能收敛,可采取以下方法。
-
不再将 $x_{op} + \delta x^*$作为下一个操作点,而是使用 $x_{op} +\alpha \delta x^*, \alpha \in [0,1] $。 通过线搜索,找到最优的α,使收敛性质更加稳健。
-
使⽤列文伯格-马夸尔特(Levenberg-Marquardt)改进⾼斯⽜顿法
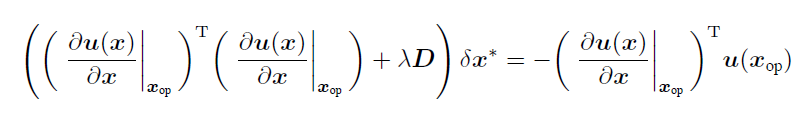
- 列文伯格-马夸尔特(Levenberg-Marquardt)
当 $\lambda$ 趋向$0$,是高斯牛顿法; 当 $\lambda$ 趋向$+\infty$,海塞矩阵的影响力减小,是梯度下降法。
MAP-End
将e线性化近似,代入高斯牛顿法。
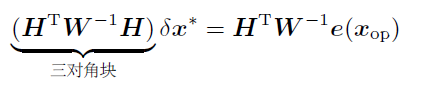

在LG系统中,对运动/观测方程求导得到梯度,也就是A,C。在NLNG系统中,一样用梯度F,G,这里是雅可比。
Bayesian Inference
和LG系统中的过程几乎一样,也和NLNG递归估计中的IEKF一样(IEKF是递归的是知道过去现在求现在将来,这里是批量的是知道全部)。
1.先验 2.观测 3.联合分布 4.后验 (高斯推断)
-
先验
线性化运动模型
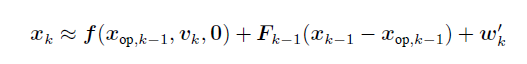
和LG时一样的做法,展开每一个k以后,整理成矩阵形式

先验均值和方差:
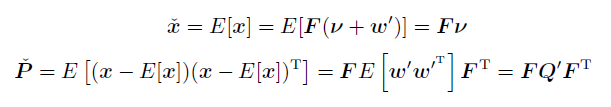
-
观测
线性化观测模型
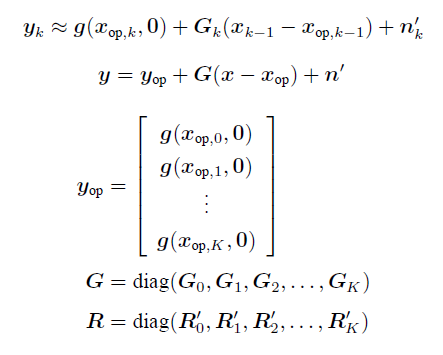
观测均值和方差:
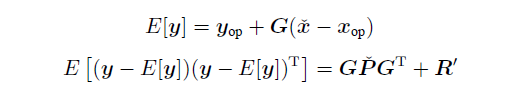
-
联合分布
联合分布需要 x均值,y均值,x协方差,y协方差(这四项就是上面计算的),还需要xy的协方差即:
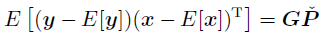
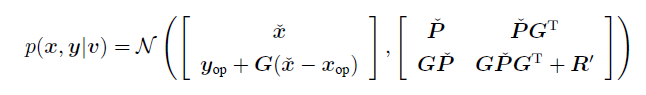
-
后验(通过高斯推断)
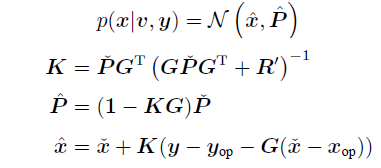
和LG中一样,将均值部分通过SMW重新组织:
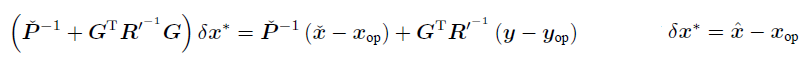
代入先验部分:
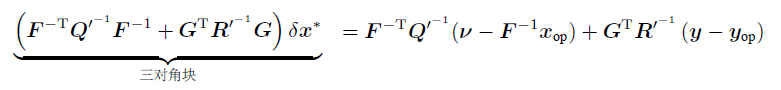
-
成立成矩阵形式:
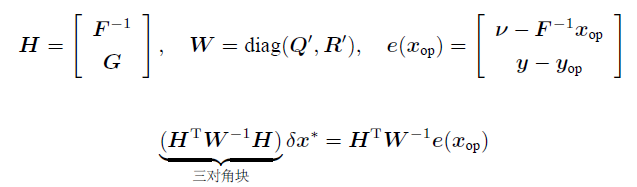
由于我们选择了迭代地对最优估计的均值进⾏重新线性化,从⽽导致了贝叶斯⽅法与MAP 具有相同的“均值”。这个现象在之前的IEKF 章节就出现了。
我们还可以想象,在批量式优化中,如果不采⽤线性化的⽅法(⽽是采⽤如采⽤粒⼦滤波、sigmapoint 变换等⽅法)来计算更新方程所需的矩,得到的结论是不⼀样的,
最大似然估计
略了
总结
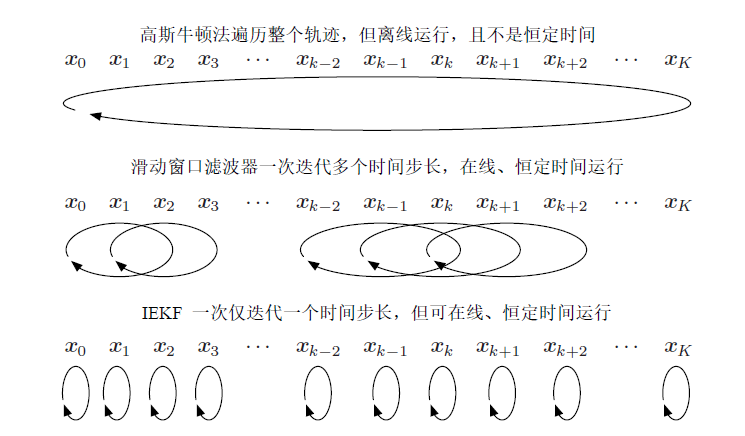
高斯牛顿:代价高,一次算一批,准确度高
IEKF:代价低,一次迭代一个,没高斯牛顿准确
14.01.2021 完结
SER目录
| SER目录 | ||
|---|---|---|
| SER-1 | K2 - 基础概率论 | |
| SER-2 | K3 - LG系统下Batch/Smoother | |
| SER-3 | K3 - LG系统下Recursive Filter | |
| SER-4 | K4 - NLNG系统下Recursive Filter | |
| SER-5 | K4 - NLNG系统下Batch | |
| SER-6 | K5 - 偏差,匹配和外点 |