唤醒矩阵运算

对于不深入学习线代已多年的人来说，需要记录一些简单的矩阵运算帮助回忆和理解。

Determinant

$det({\begin{bmatrix}a_{1,1}&a_{1,2}\\\ a_{2,1}&a_{2,2}\end{bmatrix}})=a_{1,1}a_{2,2}-a_{1,2}a_{2,1}$

Eigenvalue and -vector

$Av=\lambda v$

$(A-\lambda I) x = 0 \Rightarrow det(A-\lambda I) = 0 \Rightarrow \lambda \Rightarrow x $

Diagonalize

$P^{-1}AP = {\begin{bmatrix}\lambda_1 & 0 & \cdots & 0\\\ 0 & \lambda_2 & \cdots & 0 \\\ \vdots & \vdots & \ddots & \vdots \\\ 0 & 0 & \cdots & \lambda_n\end{bmatrix}}$ with $ P = [v_1, v_2, \cdots, v_n]$

$P^{-1}AP = D, A = PDP^{-1}$

Cofactor Matrix and Adjugate Matrix

$C = ((-1)^{i+j}M_{ij})_{1\leq i,j \leq n} $
- $ M_{ij}$ the determinat of the (n-1)×(n-1) matrix from A without row i and column j
$adj(A) = C^T$
- for 2×2: $adj({\begin{bmatrix}a&b\\\ c&d\end{bmatrix}})={\begin{bmatrix}d&-b\\\ -c&a\end{bmatrix}}$

Inverse Matrix

$A^{-1} = $ $\frac{adj(A)}{det(A)}$

$(AB)^{-1}=B^{-1}A^{-1}$
$(A^T )^{-1}=(A^{-1} )^T$
$det(A^{-1}) = (det(A))^{-1}$

Inverse of Diagonal Matrix: $diag(a_1, \cdots, a_n) ^ {-1} = diag(a_1^{-1}, \cdots, a_n^{-1})$

Inverse of Triangular Matrix: ${\begin{bmatrix}a&c\\\ 0&b\end{bmatrix}}{\begin{bmatrix}a&c\\\ 0&b\end{bmatrix}}^{-1} = I \Rightarrow {\begin{bmatrix}a&c\\\ 0&b\end{bmatrix}}^{-1} = {\begin{bmatrix}a^{-1}&-a^{-1}b^{-1}c\\\ 0&b^{-1}\end{bmatrix}}$

It is easier to calculate $A^{-1}$ by using the Inverse of Triangular Matrix: $A = LU, A^{-1} = U^{-1}L^{-1}$

Decomposition I

LU

$ M = LU$ with $L$ := unit lower triangular; $U$ := upper triangular （高斯消元）

$ \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] = \left[ \begin{matrix} 1 & 0 \\\ A^{-1}C & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A & B \\\ 0 & -BA^{-1}C+D \end{matrix} \right] $
$ M = UL$ with $U$ := unit upper triangular; $L$ := lower triangular（反向消元）

$ \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] = \left[ \begin{matrix} 1 & BD^{-1} \\\ 0 & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A-BD^{-1}C & 0 \\\ C & D \end{matrix} \right] $
$ M = \hat{L}\hat{U} $ with $\hat{L}$ := lower triangular; $\hat{U}$ := unit upper triangular

(和普通的LU其实是一样的，加了转置操作而已)

$ M = (M^T)^T = (L’U’)^T = U’^TL’^T = \hat{L}\hat{U}$

$ \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] = \left[ \begin{matrix} A & 0 \\\ C & -A^{-1}BC+D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & A^{-1}B \\\ 0 & 1 \end{matrix} \right] $

LDU / LDV / LDLT

$ M = LDU$ : $U,L$ := unit triangular; $D$ := diagonal matrix

先用普通LU分解使 $M = LU$, 将U分解成DV，D是U的对角元素构成的对角矩阵，V是剩下的对角线为1的上三角矩阵。
$LDL^T$

如果A是对称矩阵** (共轭对称也可，这边只考虑实对称)

$A = A^T = (LDV)^T = V^TDL^T $

其中 $V^T$是下三角矩阵， $V^T = L$。

打洞

是LU分解对应过程，等式两边同乘三角矩阵的逆即可相互转换。
高斯消元时，LU分解是row2-row1*a, 打洞是row2+ row1*a。

$ M = \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] $

先B后C (用行操作去掉B，用列操作去掉C)

row transformation $U$ 与$M=UL$相同:

$U \cdot M = \left[ \begin{matrix} 1 & -BD^{-1} \\\ 0 & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] = \left[ \begin{matrix} A-BD^{-1}C & 0 \\\ C & D\end{matrix} \right] $

column transformation $V$ 与$M= \hat{U}\hat{L} $相同:

$M \cdot V = \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & 1 \end{matrix} \right] = \left[ \begin{matrix} A-BD^{-1}C & B \\\ 0 & D \end{matrix} \right] $

together 与$M= UDL $相同:

$U \cdot M \cdot V=\left[ \begin{matrix} 1 & -BD^{-1} \\\ 0 & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & 1 \end{matrix} \right] = \left[ \begin{matrix} A-BD^{-1}C & 0 \\\ 0 & D \end{matrix} \right] $
先C后B (用行操作去掉C，用列操作去掉B) 就和$M = LU, M = \hat{L}\hat{U} 和 M=LDU$对应。

和先B后C是一样的，将操作矩阵和结果矩阵都交换对角元素的位置后，将AD互换，BC互换，即可互相转换。

row transformation $U$:

$U \cdot M = \left[ \begin{matrix} 1 & 0 \\\ -A^{-1}C & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] = \left[ \begin{matrix} A & B \\\ 0 & -BA^{-1}C+D \end{matrix} \right] $

column transformation $V$:

$M \cdot V = \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & -A^{-1}B \\\ 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} A & 0 \\\ C & -BA^{-1}C+D \end{matrix} \right] $

together:

$U \cdot M \cdot V =\left[ \begin{matrix} 1 & 0 \\\ -A^{-1}C & 1 \end{matrix} \right] \cdot \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & -A^{-1}B \\\ 0 & 1 \end{matrix} \right] = \left[ \begin{matrix} A & 0 \\\ 0 & -BA^{-1}C+D \end{matrix} \right] $

SMW Identity

$ M = \left[ \begin{matrix} A^{-1} & -B \\\ C & D \end{matrix} \right] $ （the Matrix used in 《SER》）

很简单把 M 写成 LDU 和 UDL 的形式，再分别求逆，再化简，得到了两个矩阵，两个矩阵对应的4个元素相等。

SMWI

Schur Complement

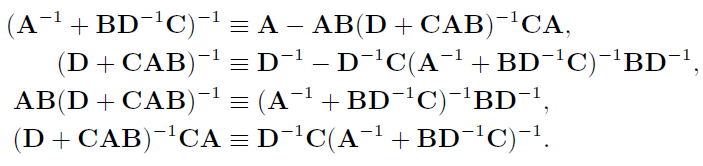
$ M = \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] $

The Schur Complement of D is: $A-BD^{-1}C$ （已出现在先B后C打洞及UL分解中）

舒尔补即用列操作给C打洞: $V = \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & 1 \end{matrix} \right]$

Wiki上用了 $L = \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & D^{-1} \end{matrix} \right] = V \cdot \left[ \begin{matrix} 1 & 0\\\ 0 & D^{-1} \end{matrix} \right]$ 其实都是一样的。用V的话能使M直接分解成UDL的形式。

$M \cdot V = \left[ \begin{matrix} A & B \\\ C & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & 1 \end{matrix} \right] = \left[ \begin{matrix} A-BD^{-1}C & B \\\ 0 & D \end{matrix} \right] =N $

$M^{-1} = V \cdot N^{-1}$

$N = \left[ \begin{matrix} SchCom & B \\\ 0 & D \end{matrix} \right] \overset{UL分解}{=} \left[ \begin{matrix} 1 & BD^{-1} \\\ 0 & 1 \end{matrix}\right] \cdot \left[\begin{matrix} SchCom & 0 \\\ 0 & D \end{matrix} \right]$

$M = N \cdot V^{-1} = \left[ \begin{matrix} 1 & BD^{-1} \\\ 0 & 1 \end{matrix}\right] \cdot \left[\begin{matrix} SchCom & 0 \\\ 0 & D \end{matrix} \right] \cdot \left[ \begin{matrix} 1 & 0\\\ CD^{-1} & 1 \end{matrix} \right]$

$M^{-1} = V \cdot N^{-1} = \left[ \begin{matrix} 1 & 0\\\ -CD^{-1} & 1 \end{matrix} \right] \cdot {\left[\begin{matrix} {SchCom} ^{-1} & 0 \\\ 0 & D^{-1} \end{matrix} \right]}\cdot {\left[ \begin{matrix} 1 & -BD^{-1} \\\ 0 & 1 \end{matrix}\right] }$

这边的变形途径很多很多，反正是写出M的UDL形式即可。

舒尔补的意义参见多维高斯分布。

Decomposition II

Cholesky 分解

如果A是正定对称矩阵** (共轭对称也可，这边只考虑实对称)

首先 $A = LDL^T$

其中 $D = diag(d_{11}, d_{22}, d_{nn})$

令 $D^{\frac{1}{2}} = diag(\sqrt{d_{11}}, \sqrt{d_{22}}, \sqrt{d_{nn}})$

$ A = LD^{\frac{1}{2}}D^{\frac{1}{2}}L^T$，令 $M = LD^{\frac{1}{2}}$，

则 $ A = MM^T$, 其中 M 是下三角矩阵乘对角矩阵还是下三角矩阵。

即 $A = L L^T$形式。

Cholesky 算法

用字母K,k,M,m表示Cholesky分解，即

$K = MM^T$

$\left[ \begin{matrix} k_{11} & \cdots & k_{1n} \\\ \vdots & \ddots & \vdots \\\ k_{n1} & \cdots & k_{nn} \end{matrix} \right]= \left[ \begin{matrix} m_{11} & & \\\ \vdots & \ddots & \\\ m_{n1} & \cdots & m_{nn} & \end{matrix} \right] \left[ \begin{matrix} m_{11} & \cdots & m_{n1} \\\ & \ddots & \vdots \\\ & & m_{nn} \end{matrix} \right]$

对于第1行第1列

$k_{11} = m_{11} \cdot m_{11} \Rightarrow m_{11} = \sqrt{k_{11}}$ (*只考虑对角线为正)
对于第1行第j列 = 第j行第1列

$k_{1j} = \left[ \begin{matrix} m_{11} & 0 & \cdots \end{matrix} \right] \left[ \begin{matrix} m_{j1} \\\ \vdots \\\ \vdots \end{matrix} \right] = m_{11} \cdot m_{j1} \Rightarrow m_{j1} = \frac{k_{11}}{m_{11}}$
对于第2行第2列

$k_{22} = \left[ \begin{matrix} m_{21} & m_{22} & 0 & \cdots \end{matrix} \right] \left[ \begin{matrix} m_{21} \\\ m_{22} \\\ 0 \\\ \vdots \end{matrix} \right] = m_{21}^2 + m_{22}^2 \Rightarrow m_{22} = \sqrt{k_{22} - m_{21}^2}$
对于第2行第j列

$k_{2j} = \left[ \begin{matrix} m_{21} & m_{22} & 0 & \cdots \end{matrix} \right] \left[ \begin{matrix} m_{j1} \\\ m_{j2} \\\ \vdots \\\ \vdots \end{matrix} \right] = m_{21} \cdot m_{j1} + m_{22} \cdot m_{j2} \Rightarrow m_{j2} = \frac{k_{2j}-m_{21} m_{j1} }{m_{22}}$
对于第i行第i列

$k_{ii} = \left[ \begin{matrix} m_{i1} & m_{i2} & \cdots & m_{ii} & 0 & \cdots \end{matrix} \right] \left[ \begin{matrix} m_{i1} \\\ m_{i2} \\\ \vdots \\\ m_{ii} \\\ 0 \\\ \vdots \end{matrix} \right] = m_{11}^2 + m_{22}^2 + \cdots + m_{ii}^2 $

其中 $m_{i1}$ 至 $m_{i(i-1)}$ 即 $m_{1i}$ 至 $m_{(i-1)i}$ 已求得。

$ m_{ii} = \sqrt{k_{ii} - \sum_{j=1}^{i-1}m_{ij}^2}$
对于第i行第j列

$ m_{ij} = $ $\frac{k_{ij}- \sum_{p=1}^{i-1}m_{ip} m_{jp} }{m_{ii}}$

数学需要的不是天赋，而是少量的自由想象