Image by Hands off my tags! Michael Gaida from Pixabay
传感器 测量

Smart Sensing-01

测量系统和误差

Posted by Yvan on October 13, 2021

Measuring System

Physical measurand → Sensing element → Signal modification subsystem → Indicator or Recorder

温度计： 温度 T → 水银/酒精 → 玻璃管，玻璃泡…组成了温度计 → 读数

Test Stands

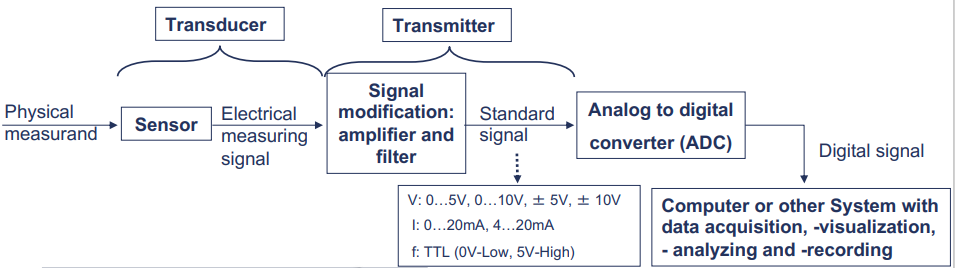
image-20211013210016810

比如 在研究上运用的NI的设备和LabVIEW，在工业上运用PLC系统

Terms

参考 传感器术语 form NI.com

True & Measurement Value

  1. 永远想得到但是永远得不到的True Value， 只有估计值
  2. 在Measurement Value 和True Value之间总是有误差measurement error

Random & Systematic Error

error = measured value - true value: 不只是测量系统自身的问题，是整个测量过程带来的。

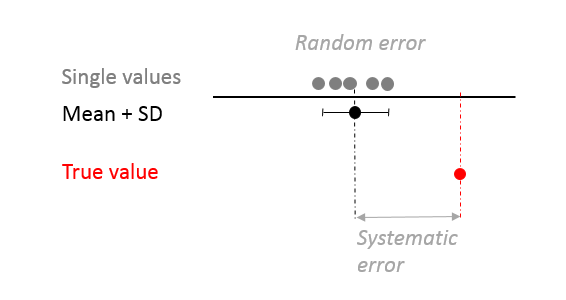
From everyday laboratory work: Systematic and random errors

All measurements have some degree of uncertainty - ppt video online download

  1. random error caused by the lack of repeatability

    = reading - average of reading

    每次测量都会有小误差(比如 刻度尺读数)= 不精确

    改善：多次重复取平均等。

  2. systematic error consistent repeatable

    = average of reading - true value

    平均测量值和实际值的误差 = 不准确

    改善：提升系统。

    1. gradient / gain error 斜率

    2. offset error 偏移

    3. nonlinearity

    4. hysteresis 迟滞现象/滞回

      增加input和减少input的output变化是不同的。下图是理想化橡皮筋伸缩的情况：橡皮筋不完全满足线性弹簧的胡克定律(F=kx)。经典的滞回还有 磁滞 和 施密特触发器 Schmitt Trigger。

      img

    5. response sensitivity

    6. measuring range

Measurement Range

  1. span = 上界-下届
  2. 超过range的测量值不是有效的测量值
  3. 每个测量系统都有特定的测量界限

Accuracy → Systematic Error

  1. 测量值和实际值的接近度

  2. 通常测量系统或传感器的生厂商定义了产品的不准确率 ±0.01mA之类的

  3. 不准确率/测量误差 通常被描述成 percentage of full scale (% FS), 少数情况是 percentage of reading (% RD)

    区别：Accuracy: % Full Scale vs. % Reading form massflow-online.com

    1. 全尺度误差：不管测量值是多少，始终有全尺度*百分数的固定误差
    2. 读数误差：存在是读数*百分数的误差
    3. 比如 一个测量范围是 5kg的秤 标注 10%FS的情况，显示2kg的东西实际可能是1.5-2.5kg；标注 10%RD的情况，显示2kg的东西实际是1.8-2.2kg

Precision → Random Error

  1. 高精确率意味着：输入不变，输出不变；即相同条件下，每次测量都能获得相同值
  2. 与准确率无关

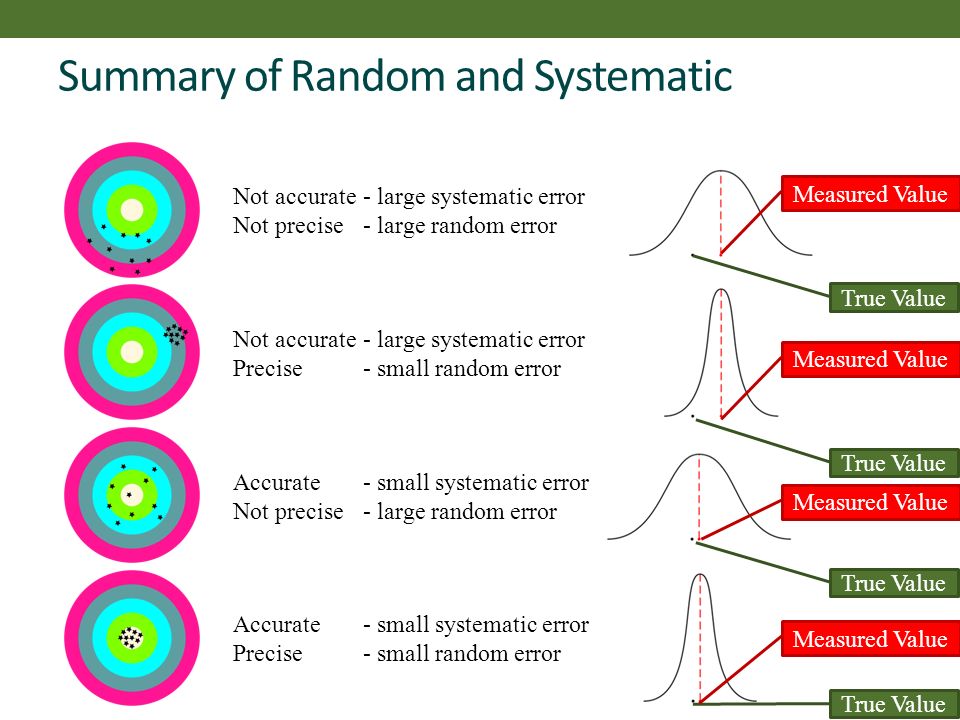
INTRODUCTORY LECTURE 3 Lecture 3: Analysis of Lab Work Electricity and Measurement (E&M)BPM – 15PHF ppt download

Resolution

定义了输入可以被分辨/测量/显示的最小变化, 比如厨房秤 1g

Sensitivity

Sensitivity

  1. ratio 输入变化的比例 和输出变化的比例相同
  2. 线性系统比例固定

Uncertainty

1 Dimension

  1. Type [1]

    如何描述这个不确定性

    1. Determinism 确定

    2. Statistical

    3. Scenario

    4. Qualitative

    5. Recognized Ignorance

    6. Indeterminacy

    7. Total Ignorance

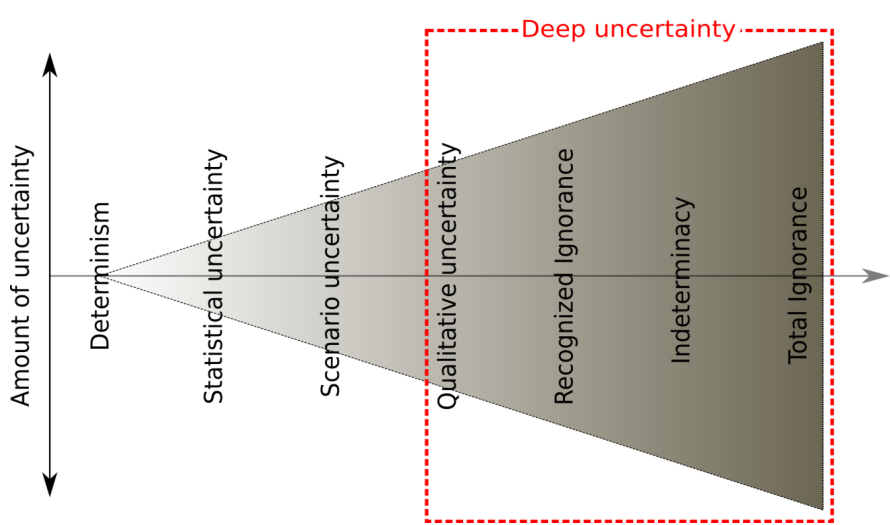
      image-20211013164210970

    越顶层的不确定性数量越少也更容易被描述，比如统计上的不确定性。

  2. Nature

    1. Epistemic - 系统性不确定性/认识性不确定性，不能知道系统的状态/忽略系统的影响因素。
    2. Variability - 自然属性不能通过操作减少。比如，不能预测投硬币的正反。
    3. Ambiguity - 不同的信息来源

  3. Location [3]

    1. model input data

    2. model parameters

    3. calibration

    4. model structure

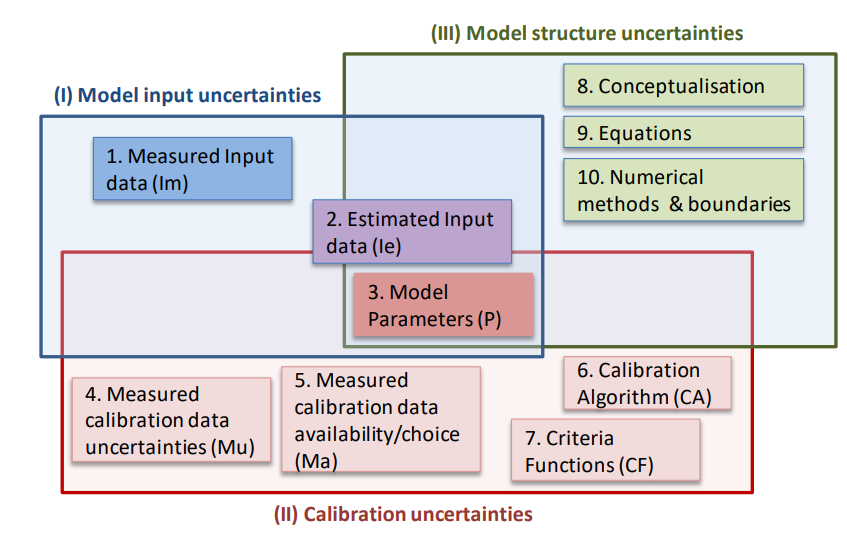
      image-20211013164143293

    5. describe uncertainties [2]

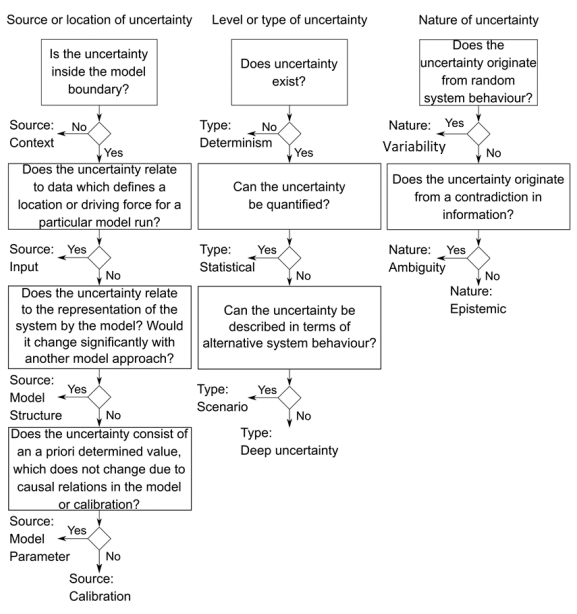
    image-20211013164344673

2 Model Calibration 校准

  1. 就像机器人状态估计里一样，我们有测量数据(比如轮子上的转速传感器)和作为标准的数据[观测数据](比如激光传感器(位移))。再比如，测量数据是降水量，标准数据是径流。通过1234循环：1 用测量数据拟合模型；2 计算出估计的标准数据；3 估计的标准数据和实际的标准数据进行比较，比如通过最小平方误差等方法；4 得到参数，然后回到1 调整模型 。最后得到最好的参数和模型。
    1. Model
    2. Calculation
    3. Comparison
    4. Parameter

  2. 不同的目标方程

    在3 Comparison中可以使用不同的目标方程：

    image-20211013165015377

    要选择合适的，可能的话运用多个，不要单独使用R2，结合图像选择。

  3. 自动校准算法

    1. Gradient method
    2. Levenberg-Marquardt-Algorithm
    3. Gauss-Newton-Method
    4. Genetic algorithm

  4. 人工校准（以降水量和径流为例）

    1. Time of maximum flow
    2. Maximum flow caused by a rain event
    3. Shape of flow curve
    4. Total volume of a rain event

  5. 验证 Validation

    类似机器学习解决过拟合Over-fitting，这里叫Over-Parametrization

3 Sensitivity Analysis

  1. Local Sensitivity Analysis

    每次只改变一个参数，其他保持不变，观察模型变化

  2. Global sensitivity Analysis

    所有参数一起改变，蒙特卡罗采样

    Equifinality 几组同一输入下，输出不变的参数

  3. No correlation between parameters

  4. Measure for Sensitivity: Sobol’ indices

    那个参数对模型影响更大

    参数的选择范围 bandwidth会影响结果

  5. 例子：Pollutant Wash-off model

4 误差传播 Propagation

  1. Law [4][5]

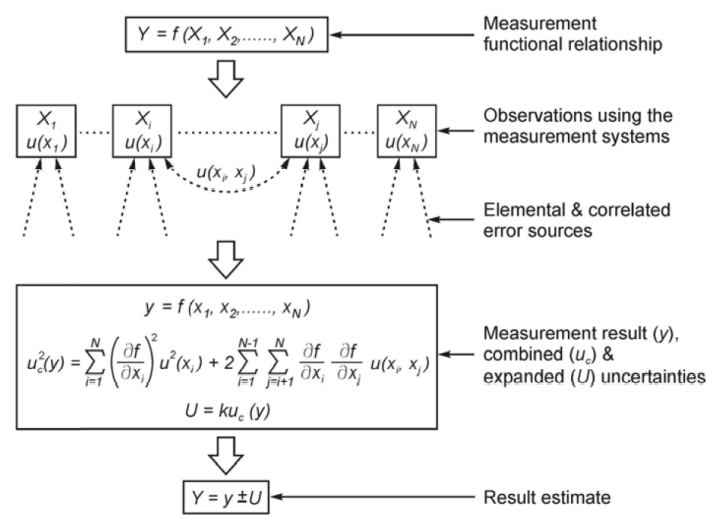
image-20211013165753829

image-20211013170134887

但对于几百个输入的模型并不试用

  1. 实际 Analysis Step [6]

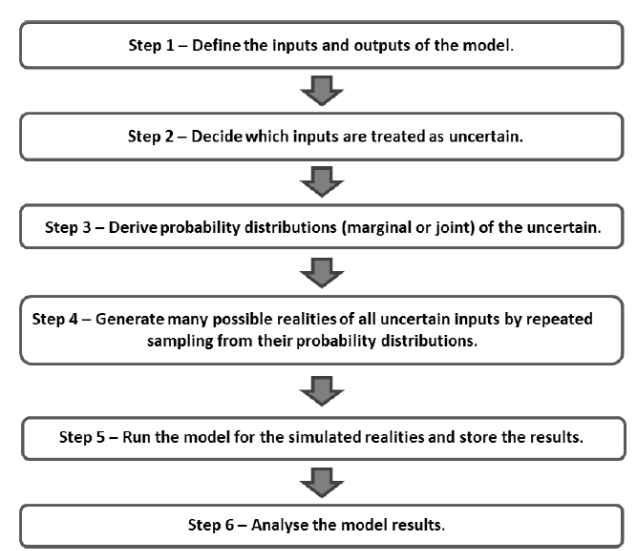
    image-20211013170303123

    • step2 不用把所有input当作uncertainty，选择影响大的: sensitive高 + 尺度大 Magnitude/Bandwidth范围大

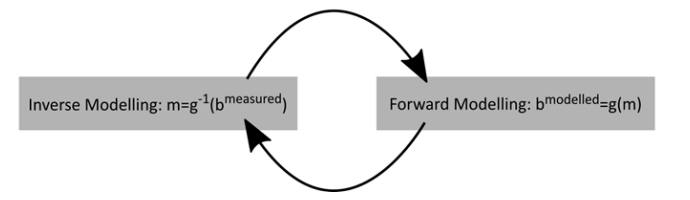
    • step3/4 用Inverse modelling 贝叶斯 / Forward modelling 蒙特卡洛

      image-20211013170657724

5 Handling of Uncertainty

Statistical analysis

  1. Model: accurate？
  2. Measurement: devices?
  3. Reality: Something happened?

Scenario analysis

  1. Predictive / Forecast / what if
  2. Explorative / Testing of possibilitie / what is possible
  3. Normative / Goal aspiration / how

[1] Source: Tscheikner-Gratl et al. (2017): QUICS - D6.7 A Framework for the application of uncertainty analysis. https://doi.org/10.5281/zenodo.1240926

[2] Source: Warmink et al. (2010). Identification and classification of uncertainties in the application of environmental models. Environ. Model. Softw. 25, 1518–1527. https://doi.org/10.1016/j.envsoft.2010.04.011

[3] Source: Deletic et al. (2012). Assessing uncertainties in urban drainage models. Phys. Chem. Earth 42–44, 3–10. https://doi.org/10.1016/j.pce.2011.04.007

[4] Source: Bertrand-Krajewski, J.-L., Ribeiro, A.S., Almeida, M. do C., 2011. Evaluation of uncertainties in measurements (Deliverable No. 3.1.6), PREPARED.

[5] Source: Pons (2020): Uncertainty and Sensitivity in Practice; Water and Wastewater Systems Advanced Course

[6] Source: Heuvelink, G.B.M., Cecinati, F., Lepot, M., Moreno-Rodenas, A., Sawicka, K., Torres, A., 2017. Guidelines and manuals for end-users on uncertainty propagation analysis and sampling designs (Deliverable No. 6.2), QUICS. Zenodo

CATALOG
    RELATED

    Smart Sensing
    NEW POSTS

    在服务器部署Wordpress

    用Docker部署Pantheon

    Wordpress数据库
    PHP/HTML/JS联动